Solving Wordle with Python

The game Wordle became very popular at the beginning of 2022. After playing the game a few times it became clear the hard part was coming up with words which satisfy the constraints. This is something trivial for a program to do. I was curious how well a program would do in the game.

Here is an example game solved by the program:

Overall stats:

Played 2315 games of Wordle
1 attemps: 1
2 attemps: 1
3 attemps: 762
4 attemps: 1335
5 attemps: 200
6 attemps: 16
Average attempts: 3.769
Unsolved Wordles: 0
Solved: 100%
Time spent (all 2k games): 54s

Before we begin, here is a quick overview of the algorithms described below. Each was tested on 2315 games of Wordle. These are the 2315 words used in the real game, as found in the website’s source code.

Algorithm	Solved	Average attemps	Time (2k)
Try to do a poorly as we can	97.8%	4.227	3s
“raise”, pick first	97.8%	3.909	3s
“raise”, heuristic	98.9%	3.735	3s
“earth” + “lions”, heuristic	99.2%	3.865	3s
“raise”, combo	99.7%	3.634	15m
“salet”, combo	99.52%	3.556	18m
“learn” + “sight”, combo	100%	3.769	54s
“raise”, optimal *	100%	3.705	hours

(*) optimal algorithm only simulated on 200 randomly chosen hidden words.

The basics - find possible words

I started by downloading a list of about 4000 words of length 5 and saved them to a file called words.txt. Only later on I realized I could get the list of words from the website’s source code.

I set off to build the basic outline of the program. Here is an example run of the program:

$ python3 wordle.py
Which word did you guess? ninja
What was the color of character n? b
What was the color of character i? g
What was the color of character n? g
What was the color of character j? b
What was the color of character a? b
OK, there are now 30 possible words: finer, wince, mince, hinge, pinto, cinch, piney, minty, singe, diner, winch, since, minor, dingo, vinyl, finch, lingo, bingo, windy, liner, miner, minim, minus, dingy, binge, pinky, sinew, kinky, rinse, pinch

The code looks like this:

words = load_words("words.txt")

# Set of characters allowed at each position
allowed = [set(), set(), set(), set(), set()]
# Set of characters we know must appear somewhere in the word
must_appear = set()
# Init all allowed sets with characters a..z.

possible = words
while True:
  guess = input("Which word did you guess? ")
  for i in range(len(guess)):
    # For simplicity of the example we skip error handling, for example
    # checking the input has the correct length (5 characters).
    g_char = guess[i]
    res = input(f"What was the color of character {g_char}? ")

    if res == 'b':
      # Black character. Remove it from allowed sets in all positions.
      for j in range(len(guess)):
        if g_char in allowed[j]:
          allowed[j].remove(g_char)

    if res == 'y':
      # The yellow character must appear in the word.
      must_appear.add(g_char)
      # But the yellow character cannot be at this position.
      if g_char in allowed[i]:
        allowed[i].remove(g_char)

    if res == 'g':
      allowed[i] = { g_char }

    possible = find_possible(possible, allowed, must_appear)

    print(
      f"OK, there are now {len(possible)} possible words:",
      ', '. join(possible)
    )
    if len(possible) == 1:
        exit()

And the function find_possible looks like this:

def is_possible(word, allowed, must_appear):
  for i in range(len(word)):
    if word[i] not in allowed[i]:
      return False
    for m in must_appear:
      if m not in word:
        return False
    return True

def find_possible(words, allowed, must_appear):
    return [word for word in words if is_possible(word, allowed, must_appear)]

This was fun to code and works well. However, when the program presents a list of 30 words we still have to think in order to narrow down the list. Can we make the program choose a good next word?

Choosing the next word

After a bit of experimentation I settled on the following heuristic: Choose a word which:

Has characters which don’t appear too often in the remaining words. In the ideal scenario we can imagine a word where each character is unique to just a few of the remaining words.
Has characters which are frequently used. This is the same strategy when choosing the first word.

I haven’t put much thought into this heuristic. I tested it by playing a few games on an app with unlimited games of Wordle. It worked reasonably well - it would solve almost all Wordles I tried.

In Python:

# So we know which characters are the most common
def character_frequencies(words):
  freq = {}
  for word in words:
    for char in word:
      if char in freq:
        freq[char] = freq[char] + 1
      else:
        freq[char] = 1
  return freq

# Assign a score to each suggestion
def suggestion_score(suggestion, possible, freq):
  score = 0
  for c in suggestion:
    for p in possible:
      if c in p:
        # The more words this character appears in
        # the lower score it gets.
        break
    # The more common character this is across our
    # dictionary the higher score it gets. We want
    # to avoid using obscure characters.
    score = score + freq[c]
  return score

# Choose a few suggestions with a high score
def suggestions(words, possible, allowed, freq):
  # We also removed all words from the list which were
  # a permutation of another word. Omitted for brevity.
  suggestion_words = [w for w in words if satisfies_allowed(w, allowed)]
  suggestions = [(w, suggestion_score(w, possible, freq)) for w in suggestion_words]
  suggestions_sorted = sorted(suggestions, key=lambda t: t[1], reverse=True)[:3]
  # Return the top 3 suggestions
  return [w for (w, s) in suggestions_sorted]

def satisfies_allowed(word, allowed):
  for i in range(len(word)):
    if word[i] not in allowed[i]:
      return False
  return True

Now all we need to do is add this as the last step into our main loop:

print(
  f"How about:",
  ', '.join(suggestions(words, possible, allowed, freq))
)

The program now suggests the next word and still lets me choose something else if I want to:

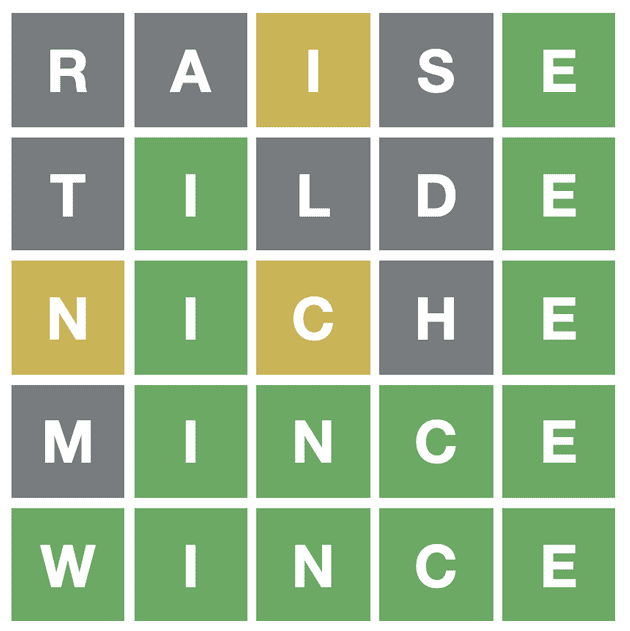
Which word did you guess? raise
...
OK, there are now 25 possible words: biome, tilde, wince, movie, mince, hinge, ...
How about: tilde, lithe, clone
What word did you guess? tilde
...
OK, there are now 10 possible words: biome, wince, mince, hinge, pique, ...
How about: niche, mince, hinge
What word did you guess? niche
...
OK, there are now 2 possible words: wince, mince

The number of options goes down: 25 -> 10 -> 2. At this point it’s a 50-50 guess so we can exit the program and try one of the remaining words.

Let’s evaluate

Now you might be wondering: OK, so the program solved the Wordle above in 5 attemps. How good is it really?

It’s time to implement our own game of Wordle. We choose a hidden word. Then we let the program guess until it is left with exactly one remaining word or fails. We count the number of attempts the program needed.

stats = {}

for hidden_word in words:
  attempts = simulate_wordle(hidden_word)
  if attempts not in stats:
    stats[attempts] = 1
  else:
    stats[attempts] = stats[attempts] + 1

The function simulate_wordle is almost the same as our main loop above. The only difference is instead of asking the user for the colors of the letters from the website, we return the colors because we know what the hidden word is:

# Returns the colors, same way the website would.
def try_guess(guess, hidden_word):
  if len(guess) != len(hidden_word):
    raise "Guess and hidden word must have the same length"
  res = ""
  for i in range(len(guess)):
    if guess[i] == hidden_word[i]:
      res = res + "g"
    elif guess[i] in hidden_word:
      res = res + "y"
    else:
      res = res + "b"
  return res

And our simulation loop looks almost the same as our interactive loop:

# simulate.py

def simulate_wordle(hidden_word, words):
  # Reset our game state
  allowed = [set(), set(), set(), set(), set()]
  must_appear = set()
  for allowed_set in allowed:
      for c in freq.keys():
          allowed_set.add(c)

  possible = words
  guess = 'raise'
  for attempt in range(MAX_ATTEMPTS):
    res = try_guess(guess, hidden_word)

    if res == 'g' * len(guess):
      # All green. Solved in this many attempts.
      return attempt + 1

    # ... handle colors the usual way by updating our state

    possible = find_possible(possible, allowed, must_appear)
    if len(possible) == 1:
      guess = possible[0]
    else:
      # The better this function, the better our program will do.
      guess = suggestions(words, possible, allowed, freq)[0]

We can now run simulate.py to see how our program does. Really we are evaluating how good our function suggestions is. Everything else is fixed and defined by the rules of the game.

We evaluate against the 2315 words the Wordle games uses, copied from the website’s source code - easy to see by inspecting the source code in the browser.

Without further ado, here are the stats:

(Starting word: "raise")
Played 2315 games of Wordle
1 attemps: 1
2 attemps: 101
3 attemps: 785
4 attemps: 911
5 attemps: 379
6 attemps: 106
Average attempts: 3.825
Unsolved Wordles: 32
Solved: 98.60%
Time spent: 9s

Now let’s try a small tweak. Instead of choosing a suggestion from all the words in the dictionary, let’s always suggest a word which is one of the remaining possible words. We might get lucky:

guess = suggestions(possible, possible, allowed, freq)[0]

Indeed this helps a little, and runs about 3x faster:

(Starting word: "raise")
Played 2315 games of Wordle
1 attemps: 1
2 attemps: 131
3 attemps: 858
4 attemps: 875
5 attemps: 331
6 attemps: 93
Average attempts: 3.735 (was 3.825)
Unsolved Wordles: 26 (was 32)
Solved: 98.86%
Time spent: 3.19s

Different starting word

You might be wondering where I got the starting word “raise” from. I found it on Reddit. Someone wrote a program to look for the best starting word and found “raise”.

Out of curiosity, let’s compare to the popular starting word “adieu”. The word “adieu” does slightly worse:

(Starting word: "adieu")
Played 2315 games of Wordle
2 attemps: 80
3 attemps: 708
4 attemps: 1000
5 attemps: 384
6 attemps: 103
Average attempts: 3.878 ("raise" was 3.735)
Unsolved Wordles: 40 ("raise" was 26)
Solved: 98.24%

Notice “adieu” is never the hidden word in Wordle - we never got all green on the first guess. The game source code has two lists: 2315 possible hidden words, and about 10k words which it accepts as guesses.

Now, let’s try a terrible starting word to see how much the starting word matters:

(Starting word: "jolly")
Played 2315 games of Wordle
1 attemps: 1
2 attemps: 28
3 attemps: 389
4 attemps: 1051
5 attemps: 630
6 attemps: 166
Average attempts: 4.227 ("raise" was 3.735 - big difference)
Unsolved Wordles: 50 ("raise" was 26)
Solved 97.79%

Does our heuristic actually do much?

Now we’ve looked at the effect of the starting word let’s look at how much the heuristic helps. Let’s simplify by throwing away our heuristic and suggest the first possible word instead:

guess = possible[0]

The stats still don’t look too bad given there is almost no code - just implementing the rules of the game and choosing the first word that’s available! I didn’t expect simply picking any word from the remaining ones would work quite well. This would be a really fun exercise for a programming intro class!

(Starting word: "raise")
Played 2315 games of Wordle
1 attemps: 1
2 attemps: 131
3 attemps: 678
4 attemps: 865
5 attemps: 445
6 attemps: 146
Average attempts: 3.909 (with heuristic was 3.735)
Unsolved Wordles: 49 (with heuristic was 26)
Solved: 97.84%
Time spent: 2.73s

OK, it’s good to know our heuristic guess = suggestions(possible, possible, allowed, freq)[0] does improve the performance, although not by a huge amount.

Trying to do as poorly as we can

If we throw away our heuristic AND choose a bad starting word, we still solve 96% of all Wordles, on average in 4.351 attempts. Interesting! This is really the lowest bar any program should meet. It would be difficult to do worse than this.

Back on track - two starting words

Back on track, let’s continue improving. Can we get to 100%?

As a reminder, here is our best result so far, using “raise” (found on Reddit) plus our heuristic to recommend the next word:

(Starting word: "raise")
Average attempts: 3.735
Unsolved Wordles: 26
Solved: 98.86%
Time spent: 3.19s

Let’s try something different - we always start with “earth” as the first word and “lions” as the next word. From third attempt onwards our program continues suggesting words as usual:

(Starting words: "earth", "lions")
Average attempts: 3.865 (A bit worse.)
Unsolved Wordles: 18 (Best so far!)
Solved 99.22% (Best so far!)

There’s a tradeoff here but I would call this an improvement. If we go with “learn” and “sight” we get a very similar result.

How did we come up with “earth”, “lions” and “learn”, “sight”? Wrote a separate script which uses brute force to look at all pairs of words in the dictionary and chooses those pairs which cover 10 common characters. Here are some examples you can use as two starting words:

earth, lions
coast, liner
sonic, alert
stale, rhino

Optimal algorithm

At this point I knew I was close to hitting the limit of the current approach. Solving 99.22% Wordles in 3.865 attempts on average is good but can we do better?

I had a look at Reddit and saw someone explain the optimal algorithm:

Use a fixed starting word. I stuck with “raise” which was recommended in a different Reddit thread.
Choose one word w from the dictionary. Imagine this is our next guess. Simulate one round of Wordle. We don’t know what the hidden word is but we look at all the possibilities of the hidden word. For each possible hidden word, we simulate one round and see how many words would be left after this round.
This gives us a list of “scores” for w. Lower numbers are better. The list will look something like this: [5, 8, 1, 25]. The list will contain one item per each possible hidden word. The value for that hidden word is the number of remaining words after the next round - once we guess w.
Now we need to combine the numbers in the list to find out how good w was. I went with simply adding the numbers: sum([5, 8, 1, 25]). This gives us the score for w. Lower is better.
Repeat all the above for every word w in the dictionary.
Return w with the lowest score. This will be our next guess.

In Python:

import copy
from possible import find_possible

def suggestion_optimal(words, possible, allowed, must_appear):
  lowest_total = 1000*1000
  best_guess = ''
  # Imagine we guess a word, see how many options would remain on average
  for w in words:
    total_for_guess = 0
    for hidden_word in possible:
      new_count = new_possible_count(possible, w, hidden_word, allowed, must_appear)
      total_for_guess = total_for_guess + new_count

      if total_for_guess < lowest_total:
        lowest_total = total_for_guess
        best_guess = w

    print(f"Looked at {len(words)} words. Best is {best_guess} with {lowest_total / len(possible):.2f} remaining words on average")

    return best_guess

def new_possible_count(possible, guess, hidden_word, allowed, must_appear):
  new_allowed = copy.deepcopy(allowed)
  new_must_appear = copy.deepcopy(must_appear)

  # Once again we simulate one round of Wordle.
  # Should really extract and reuse this lol
  for i in range(len(guess)):
    g_char = guess[i]
    if g_char == hidden_word[i]:
      # Green
      new_allowed[i] = { g_char }
    elif g_char in hidden_word:
      # The yellow character must appear in the word
      new_must_appear.add(g_char)
      # But the yellow character cannot be at that position
      if g_char in new_allowed[i]:
        new_allowed[i].remove(g_char)
    else:
      for j in range(len(guess)):
        if g_char in new_allowed[j]:
          new_allowed[j].remove(g_char)

  return len(find_possible(possible, new_allowed, new_must_appear))

This performs really well but it is very slow. So slow that a single game of Wordle can take more than a minute to solve. There’s no hope to simulate all 2315 games on my laptop.

That said, I simulated 200 randomly chosen words out of the 2315, on 5 CPUs simulating 40 games each. The result looks great - we get a perfect 100% score!

Starting word: "raise"
Played 200 games of Wordle
Statistics:
2 attemps: 5
3 attemps: 65
4 attemps: 114
5 attemps: 16
Average attempts: 3.705 (Best so far)
Unsolved Wordles: 0
Solved 100.00% (Great!)
Time spent: Hours of single CPU time.

Why is this so slow? The majority of time is spent on the second guess. After we guess “raise” we are left with, say, 20-100 words. Here’s what we do:

For each of the 100 possible words:
  For each 2315 words w:
    Copy game state. That is 5 sets of allowed characters, up to 26 characters each.
    Compare w to possible word, update game state
    Find possible words for the next round:
      For each of the 100 words, see if it matches game state:
        1-5 set lookups
        0-5 lookups for yellow letters

We copy the game state 231k times, and we call is_possible 23 million times. I also chose Python for the job not knowing the computation would get intense :) I’m happy with choosing Python though because writing the code is fun and quick. I also wanted to practice Python as I don’t use it daily.

Time to combine the approaches

The optimal algorithm works well. It is very slow but actually usable for a single game of Wordle. You just have to wait for a minute for a second guess 😃 However, we cannot evaluate this algorithm on all 2315 games in a reasonable amount of time.

What we are going to do is use our heuristic described earlier to choose a smaller list of 50 possible guesses:

narrowed_list = suggestions(possible, possible, allowed, freq)

Then we run the optimal algorithm, passing in the narrowed_list instead of the whole dictionary:

narrowed_list = suggestions(possible, possible, allowed, freq)
guess = suggestion_optimal(narrowed_list, possible, allowed, must_appear)

That’s it. Instead of 100 x 2315 we are now doing 10 x 50, so everything runs about 46x faster. It is still painfully slow with only about 2 games per second. After waiting for 15 minutes, let’s see the results:

Starting word: "raise"
Played 2315 games of Wordle
1 attemps: 1
2 attemps: 79
3 attemps: 909
4 attemps: 1117
5 attemps: 178
6 attemps: 24
Average attempts: 3.634
Unsolved Wordles: 7
Solved 99.70%
Time spent: 15 minutes

And with “salet” as the starting word:

2 attemps: 148
3 attemps: 975
4 attemps: 967
5 attemps: 179
6 attemps: 35
Average attempts: 3.556
Unsolved Wordles: 11
Solved 99.52%

This is the best result I was able to fully evaluate so far. The totally optimal algorithm is way too slow. This one runs about 2 games per second and if we discount the slow optimal algorithm, this one is the best. It beats the heuristic-only approach both in average attempts and in number of solved Wordles.

Let’s try one more thing: a combo approach but using two harcoded starting words: “learn” and “sight”:

1 attemps: 1
2 attemps: 1
3 attemps: 762
4 attemps: 1335
5 attemps: 200
6 attemps: 16
Average attempts: 3.769
Unsolved Wordles: 0
Solved 100%
Time spent: 54s

Turns out using “learn” and “sight” as the first two words works well for the Wordle data set. If we chose “earth” and “lions” we’d end up with 7 unsolved Wordles.

This is the best solution I was able to fully evaluate on all 2315 games. It solves all Wordles in 54s. The number of attempts is 3.769 on average.

Summary

Here are the stats for all the algorithms described, for 2315 games of Wordle each:

Algorithm	Unsolved	Average attemps	Time (2k)
Try to do a poorly as we can	50	4.227	3s
“raise”, pick first	49	3.909	3s
“raise”, heuristic	26	3.735	3s
“earth” + “lions”, heuristic	18	3.865	3s
“raise”, combo	7	3.634	15m
“salet”, combo	11	3.556	18m
“learn” + “sight”, combo	0	3.769	54s
“raise”, optimal *	0	3.705	hours

(*) optimal algorithm only simulated on 200 randomly chosen hidden words.

Which option from the table above would you want to use?